fuck this
This commit is contained in:
parent
97dc43c792
commit
24428eda95
10 changed files with 124 additions and 46 deletions
Binary file not shown.
|
Before 
(image error) Size: 86 KiB After 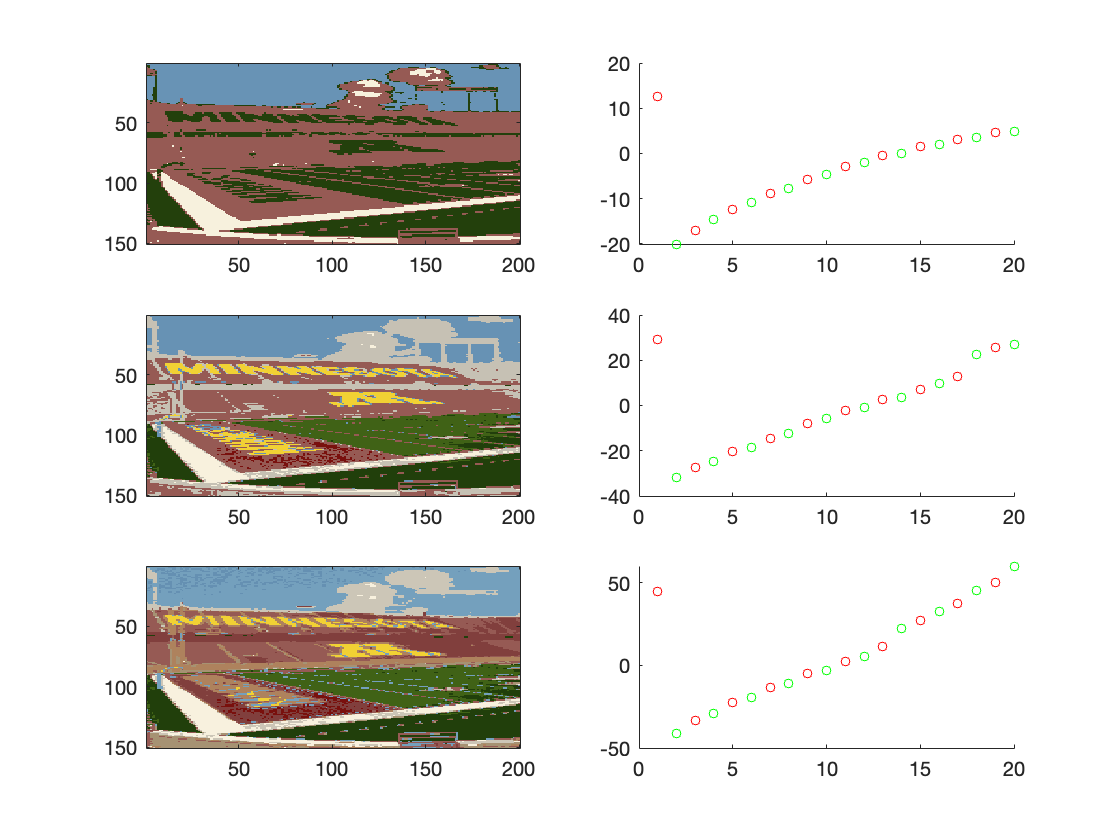
(image error) Size: 58 KiB 

|
BIN
assignments/hwk03/2c.png
Normal file
BIN
assignments/hwk03/2c.png
Normal file
Binary file not shown.
|
After 
(image error) Size: 44 KiB |
BIN
assignments/hwk03/2e.png
Normal file
BIN
assignments/hwk03/2e.png
Normal file
Binary file not shown.
|
After 
(image error) Size: 26 KiB |
|
|
@ -24,15 +24,13 @@ function [h, m, Q] = EMG(x, k, epochs, flag)
|
|||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% TODO: Initialise cluster means using k-means
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
[~, ~, ~, D] = kmeans(x, k);
|
||||
[idx, m] = kmeans(x, k);
|
||||
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% TODO: Determine the b values for all data points
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
for i = 1:num_data
|
||||
row = D(i,:);
|
||||
minIdx = row == min(row);
|
||||
b(i,minIdx) = 1;
|
||||
b(i, idx(i)) = 1;
|
||||
end
|
||||
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
|
|
@ -40,17 +38,17 @@ function [h, m, Q] = EMG(x, k, epochs, flag)
|
|||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
pi = zeros(k, 1);
|
||||
for i = 1:k
|
||||
pi(i) = sum(b(:, i));
|
||||
pi(i) = sum(b(:, i)) / num_data;
|
||||
end
|
||||
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% TODO: Initialize the covariance matrix estimate
|
||||
% further modifications will need to be made when doing 2(d)
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
m = zeros(k, dim);
|
||||
% m = zeros(k, dim);
|
||||
for i = 1:k
|
||||
data = x(b(:, i) == 1, :);
|
||||
m(i, :) = mean(data);
|
||||
% m(i, :) = mean(data);
|
||||
S(:, :, i) = cov(data);
|
||||
end
|
||||
|
||||
|
|
@ -65,7 +63,7 @@ function [h, m, Q] = EMG(x, k, epochs, flag)
|
|||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% TODO: Store the value of the complete log-likelihood function
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
Q(2*n - 1) = Q_step(x, m, S, k, pi, h);
|
||||
Q(2*n - 1) = Q_step(x, m, S, k, pi, h, flag);
|
||||
|
||||
|
||||
%%%%%%%%%%%%%%%%
|
||||
|
|
@ -77,7 +75,7 @@ function [h, m, Q] = EMG(x, k, epochs, flag)
|
|||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% TODO: Store the value of the complete log-likelihood function
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
Q(2*n) = Q_step(x, m, S, k, pi, h);
|
||||
Q(2*n) = Q_step(x, m, S, k, pi, h, flag);
|
||||
end
|
||||
|
||||
|
||||
|
|
|
|||
|
|
@ -27,4 +27,22 @@ function [h] = E_step(x, h, pi, m, S, k)
|
|||
h(j, :) = parts(j, :) ./ s;
|
||||
end
|
||||
|
||||
|
||||
% parts = zeros(k);
|
||||
%
|
||||
% denom = 0;
|
||||
% for i = 1:k
|
||||
% N = mvnpdf(x, m(i, :), S(:, :, i));
|
||||
% for j = 1:num_data
|
||||
% parts(i) = parts(i) + pi(i) * N(j);
|
||||
% end
|
||||
% denom = denom + parts(i);
|
||||
% end
|
||||
%
|
||||
% for i = 1:k
|
||||
% h(:, i) = parts(i) ./ denom;
|
||||
% end
|
||||
|
||||
|
||||
|
||||
end
|
||||
|
|
@ -47,9 +47,9 @@ function [S, m, pi] = M_step(x, h, S, k, flag)
|
|||
% Calculate the covariance matrix estimate
|
||||
% further modifications will need to be made when doing 2(d)
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
S = zeros(dim, dim, k) + eps;
|
||||
S = zeros(dim, dim, k);
|
||||
for i = 1:k
|
||||
s = zeros(dim, dim);
|
||||
s = zeros(dim, dim) + eye(dim) * eps;
|
||||
for j = 1:num_data
|
||||
s = s + h(j, i) * (x(j, :) - m(i, :))' * (x(j, :) - m(i, :));
|
||||
end
|
||||
|
|
@ -59,12 +59,18 @@ function [S, m, pi] = M_step(x, h, S, k, flag)
|
|||
% % MAKE IT SYMMETRIC https://stackoverflow.com/a/38730499
|
||||
% S(:, :, i) = (s + s') / 2;
|
||||
% https://www.mathworks.com/matlabcentral/answers/366140-eig-gives-a-negative-eigenvalue-for-a-positive-semi-definite-matrix#answer_290270
|
||||
s = (s + s') / 2;
|
||||
% s = (s + s') / 2;
|
||||
% https://www.mathworks.com/matlabcentral/answers/57411-matlab-sometimes-produce-a-covariance-matrix-error-with-non-postive-semidefinite#answer_69524
|
||||
[V, D] = eig(s);
|
||||
s = V * max(D, eps) / V;
|
||||
% [V, D] = eig(s);
|
||||
% s = V * max(D, eps) / V;
|
||||
|
||||
S(:, :, i) = s;
|
||||
end
|
||||
|
||||
if flag
|
||||
for i = 1:k
|
||||
S(:, :, i) = S(:, :, i) + lambda * eye(dim) / 2;
|
||||
end
|
||||
end
|
||||
|
||||
end
|
||||
11
assignments/hwk03/Makefile
Normal file
11
assignments/hwk03/Makefile
Normal file
|
|
@ -0,0 +1,11 @@
|
|||
|
||||
HANDIN_PDF := hw3_sol.pdf
|
||||
HANDIN_ZIP := hw3_code.zip
|
||||
|
||||
all: $(HANDIN_PDF) $(HANDIN_ZIP)
|
||||
|
||||
$(HANDIN_PDF): hw3_sol.typ
|
||||
typst compile $< $@
|
||||
|
||||
$(HANDIN_ZIP): E_step.m EMG.m M_step.m Problem2.m Q_step.m goldy.jpg stadium.jpg
|
||||
zip $(HANDIN_ZIP) $^
|
||||
|
|
@ -22,32 +22,32 @@ function [] = Problem2()
|
|||
%%%%%%%%%%
|
||||
% 2(a,b) %
|
||||
%%%%%%%%%%
|
||||
index = 1;
|
||||
figure();
|
||||
for k = 4:4:12
|
||||
fprintf("k=%d\n", k);
|
||||
% index = 1;
|
||||
% figure();
|
||||
% for k = 4:4:12
|
||||
% fprintf("k=%d\n", k);
|
||||
|
||||
% call EM on data
|
||||
[h, m, Q] = EMG(stadium_x, k, epochs, false);
|
||||
% % call EM on data
|
||||
% [h, m, Q] = EMG(stadium_x, k, epochs, false);
|
||||
|
||||
% get compressed version of image
|
||||
[~,class_index] = max(h,[],2);
|
||||
compress = m(class_index,:);
|
||||
% % get compressed version of image
|
||||
% [~,class_index] = max(h,[],2);
|
||||
% compress = m(class_index,:);
|
||||
|
||||
% 2(a), plot compressed image
|
||||
subplot(3,2,index)
|
||||
imagesc(permute(reshape(compress, [width, height, depth]),[2 1 3]))
|
||||
index = index + 1;
|
||||
% % 2(a), plot compressed image
|
||||
% subplot(3,2,index)
|
||||
% imagesc(permute(reshape(compress, [width, height, depth]),[2 1 3]))
|
||||
% index = index + 1;
|
||||
|
||||
% 2(b), plot complete data likelihood curves
|
||||
subplot(3,2,index)
|
||||
x = 1:size(Q);
|
||||
c = repmat([1 0 0; 0 1 0], length(x)/2, 1);
|
||||
scatter(x,Q,20,c);
|
||||
index = index + 1;
|
||||
pause;
|
||||
end
|
||||
shg
|
||||
% % 2(b), plot complete data likelihood curves
|
||||
% subplot(3,2,index)
|
||||
% x = 1:size(Q);
|
||||
% c = repmat([1 0 0; 0 1 0], length(x)/2, 1);
|
||||
% scatter(x,Q,20,c);
|
||||
% index = index + 1;
|
||||
% pause;
|
||||
% end
|
||||
% shg
|
||||
|
||||
%%%%%%%%
|
||||
% 2(c) %
|
||||
|
|
@ -63,14 +63,18 @@ function [] = Problem2()
|
|||
[~,class_index] = max(h,[],2);
|
||||
compress = m(class_index,:);
|
||||
figure();
|
||||
subplot(2,1,1)
|
||||
subplot(3,1,1)
|
||||
imagesc(permute(reshape(compress, [width, height, depth]),[2 1 3]))
|
||||
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% TODO: plot goldy image after using clusters from k-means
|
||||
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
||||
% begin code here
|
||||
[~, ~, ~, D] = kmeans(goldy_x, k);
|
||||
[idx, m] = kmeans(goldy_x, k);
|
||||
compress = m(idx,:);
|
||||
subplot(3,1,2)
|
||||
imagesc(permute(reshape(compress, [width, height, depth]),[2 1 3]));
|
||||
pause;
|
||||
|
||||
% end code here
|
||||
shg
|
||||
|
|
@ -84,7 +88,7 @@ function [] = Problem2()
|
|||
% plot goldy image using clusters from improved EM
|
||||
[~,class_index] = max(h,[],2);
|
||||
compress = m(class_index,:);
|
||||
figure();
|
||||
subplot(1,1,1)
|
||||
imagesc(permute(reshape(compress, [width, height, depth]),[2 1 3]))
|
||||
shg
|
||||
end
|
||||
|
|
@ -1,4 +1,4 @@
|
|||
function [LL] = Q_step(x, m, S, k, pi, h)
|
||||
function [LL] = Q_step(x, m, S, k, pi, h, flag)
|
||||
[num_data, ~] = size(x);
|
||||
LL = 0;
|
||||
for i = 1:k
|
||||
|
|
|
|||
|
|
@ -29,20 +29,20 @@ Solved as:
|
|||
|
||||
- $
|
||||
frac(diff E, diff w_(1,j)) &= - sum_t frac(diff E, diff y^t) frac(diff y^t, diff z^t_h) frac(diff z^t_h, diff w_(1,j)) \
|
||||
&= - sum_t (frac(r^t, y^t) - frac(1-r^t, 1-y^t)) (y^t (1-y^t) v_h) (x_h cases(0 "if" ww_1 dot xx <0, 1 "otherwise")) \
|
||||
&= - sum_t (r^t - y^t) v_h x_h cases(0 "if" ww_1 dot xx <0, 1 "otherwise") \
|
||||
&= - sum_t (frac(r^t, y^t) - frac(1-r^t, 1-y^t)) (y^t (1-y^t) v_1) (x_j cases(0 "if" ww_1 dot xx <0, 1 "otherwise")) \
|
||||
&= - sum_t (r^t - y^t) v_1 x_j cases(0 "if" ww_1 dot xx <0, 1 "otherwise") \
|
||||
$
|
||||
|
||||
- $
|
||||
frac(diff E, diff w_(2,j)) &= - sum_t frac(diff E, diff y^t) frac(diff y^t, diff z^t_h) frac(diff z^t_h, diff w_(2,j)) \
|
||||
&= - sum_t (r^t - y^t) v_h x_h (1-tanh^2(ww_2 dot xx)) \
|
||||
&= - sum_t (r^t - y^t) v_2 x_j (1-tanh^2(ww_2 dot xx)) \
|
||||
$
|
||||
|
||||
Updates:
|
||||
|
||||
- $Delta v_h = eta sum_t (r^t-y^t) z^t_h$
|
||||
- $Delta w_(1,j) = eta sum_t (r^t - y^t) v_h x_h cases(0 "if" ww_1 dot xx <0, 1 "otherwise")$
|
||||
- $Delta w_(2,j) = eta sum_t (r^t - y^t) v_h x_h (1-tanh^2(ww_2 dot xx))$
|
||||
- $Delta w_(1,j) = eta sum_t (r^t - y^t) v_1 x_j cases(0 "if" ww_1 dot xx <0, 1 "otherwise")$
|
||||
- $Delta w_(2,j) = eta sum_t (r^t - y^t) v_2 x_j (1-tanh^2(ww_2 dot xx))$
|
||||
|
||||
= Problem 1b
|
||||
|
||||
|
|
@ -72,10 +72,51 @@ Updates:
|
|||
|
||||
= Problem 2a + 2b
|
||||
|
||||
For this problem I see a gentle increase in the likelihood value after each of
|
||||
the E + M steps. There is an issue with the first step but I don't know what
|
||||
it's caused by.
|
||||
|
||||
In general, the higher $k$ was, the more colors there were, and it was able to
|
||||
produce a better color mapping. The last $k = 12$ had the best "resolution" (not
|
||||
really resolution since the pixel density didn't change but there are more
|
||||
detailed shapes).
|
||||
|
||||
#image("2a.png")
|
||||
|
||||
#pagebreak()
|
||||
|
||||
= Problem 2c
|
||||
|
||||
For this version, k-means performed a lot better than my initial EM step, even
|
||||
with a $k$ of 7. I'm suspecting what's happening is that between the EM steps,
|
||||
the classification of the data changes to spread out inaccurate values, while
|
||||
with k-means it's always operating on the original data.
|
||||
|
||||
#image("2c.png")
|
||||
|
||||
#pagebreak()
|
||||
|
||||
= Problem 2d
|
||||
|
||||
MLE of $Sigma_i$
|
||||
For the $Sigma$ update step, I added this change:
|
||||
|
||||
#let rtext(t) = {
|
||||
set text(red)
|
||||
t
|
||||
}
|
||||
|
||||
$
|
||||
Sigma_i &= frac(1, N_i) sum_(t=1)^N gamma(z^t_i) (x^t - u) (x^t - u)^T
|
||||
rtext(- frac(lambda, 2) sum_(i=1)^k sum_(j=1)^d (Sigma^(-1)_i)_("jj"))
|
||||
$
|
||||
|
||||
The overall maximum likelihood could not be derived because of the difficulty
|
||||
with logarithm of sums
|
||||
|
||||
= Problem 2e
|
||||
|
||||
After implementing this, the result was a lot better. I believe that the
|
||||
regularization term helps because it makes the $Sigma$s bigger which makes it
|
||||
converge faster.
|
||||
|
||||
#image("2e.png")
|
||||
Loading…
Add table
Reference in a new issue