20 KiB
| geometry | output | title | subtitle | date | author |
|---|---|---|---|---|---|
| margin=2cm | pdf_document | Exam 1 | CSCI 5607 | \today | | Michael Zhang | zhan4854@umn.edu $\cdot$ ID: 5289259 |
\renewcommand{\c}[1]{\textcolor{gray}{#1}}
Image File Formats
-
\c{(8 points) Suppose you have used your raytracing program to create an image in image file type? Other potential image file format options include: JPEG, TIFF, and GIF. Discuss the main advantages and disadvantages in converting your image from ASCII PPM to these other file types. Try to identify at least one strength and one weakness of each option.}
ASCII PPM has the obvious deficiency of not having a concise representation on disk (although P6 solves this problem). On the plus side, it is easy to represent it in a way that’s easy to debug, for example if you put double line breaks between each row in the image, and added a comment making it easy to identify rows in the image quickly.
JPEG is typically a lossy data format, which means while you can get insanely high compression resulting in lower file sizes, you also get compression artifacts which ruins the quality of the image. On the other hand, ASCII PPM is lossless and preserves the original image at original quality entirely.
Color Spaces
-
\c{(8 points) Your raytracing program generates images using an RGB color model. But RGB is not the only color space that artists or programmers use when creating or working with digital images. Identify two other color spaces that are commonly used in computer graphics or related fields. Describe their most important characteristics, and discuss how they are similar to and/or different from using an (r, g, b) representation. For each color space, try to identify at least one use case where it might be preferred over using an RGB representation and explain.}
Another color space that is typically used for computer graphics is CMYK, and YUV.
CMYK uses the secondary colors cyan, magenta, and yellow, as well as black. This is primarily used for printing, because as opposed to when light is emitted from a computer screen, reflected light from paper combines differently. When applying more ink or combining ink together, the color tends to get darker rather than lighter, so lighter base colors are preferred. The black is added since it is not possible to create pure black otherwise.
YUV is used more commonly in video formats. It uses luma, and red/blue projections of the image rather than RGB. While equally expressive as RGB, YUV is more efficient in video since the chroma of an image doesn’t change as frequently over video.
Color Compositing
-
\c{"Alpha-blending" or "color compositing" is a method for combining the colors of one image with the colors of another. A typical alpha-blending function is:
C_{final} = C_{fg} \cdot a_{fg} + C_{bg} \cdot (1 - a_{fg})whereC_{fg}is the color of the foreground pixel,Cbgis the color of the background pixel,a_{fg}is the opacity of the foreground pixel (wherea_{fg} = 1represents "fully opaque" anda_{fg} = 0represents "fully transparent"), anda_{bg}is assumed to be 1. Whena_{fg} = 0.5,C_{final} = \frac{C_{fg} + C_{bg}}{2}which is equivalent to taking the average of the foreground and background colors. Yet, the results of using alpha-blending to composite multiple transparent surfaces is different than the results of averaging their colors.}\c{Consider a pure green image and a pure blue image, each with $\alpha = 0.5$. If
C_{bg} = (0,0,0,1), what color would be obtained by:}a) \c{(3 points) compositing the blue image over background, then the green image over the result?}
In this case, compositing the blue
(0, 0, 1, 0.5)over the background(0, 0, 0, 1)would be $C_{final} = (0, 0, 1) \cdot 0.5 + (0, 0, 0) \cdot (1 - 0.5) = (0, 0, 0.5)$.Then, compositing green over this gives us: $C_{final} = (0, 1, 0) \cdot 0.5 + (0, 0, 0.5) \cdot (1 - 0.5) = (0, 0.5, 0) + (0, 0, 0.25) = \boxed{(0, 0.5, 0.25)}$.
b) \c{(2 points) compositing the green image over background, then the blue image over the result?}
The result will be the same, except with the blue and green components reversed:
\boxed{(0, 0.25, 0.5)}.\c{When
a_{bg} \ne 1, the alpha blending function becomes slightly more complicated: $a_{final} = a_{fg} + a_{bg} \cdot (1 - a_{fg})$; $C_{final} = \frac{C_{fg} \cdot a_{fg} + C_{bg} \cdot a_{bg} \cdot (1 - a_{fg})}{a_{final}}$.}c) \c{(3 points) What result do you obtain by compositing the blue image over the green image, and then compositing that result over the background?}
First, we want to composite the blue image over the green image, which both have an alpha of
0.5:a_{final} = 0.5 + 0.5 \cdot (1 - 0.5) = 0.75.Then
\begin{align*} C_{final} &= \frac{C_{fg} \cdot a_{fg} + C_{bg} \cdot a_{bg} \cdot (1 - a_{fg})}{a_{final}} \ &= \frac{(0, 0, 1) \cdot 0.5 + (0, 1, 0) \cdot 0.5 \cdot (1 - 0.5)}{0.75} \ &= \frac{(0, 0, 0.5) + (0, 0.25, 0)}{0.75} \ &= \frac{(0, 0.25, 0.5)}{0.75} \ &= (0, 0.\overline{333}, 0.\overline{666}) \end{align*}
Now, composite this over the background:
\begin{align*} C_{final} &= C_{fg} \cdot a_{fg} + C_{bg} \cdot (1 - a_{fg}) \ &= (0, 0.\overline{333}, 0.\overline{666}) \cdot 0.75 + (0, 0, 0) \cdot (1
- 0.75) \ &= (0, 0.25, 0.5) \cdot 0.75 \ &= \boxed{(0, 0.1875, 0.375)} \end{align*}
Alpha is 1 at the end because of blending with the background.
d) \c{(2 points) How does your answer in (c) differ from what you would get by simply averaging the blue and green images, and then superimposing that result over the background?}
Because the alphas are 0.5, the way you blend the images produces a more nuanced 0.75 alpha for whichever ones you blend first. So if you were to blend into the background first, the background has more of an effect on the blended image.
Viewing Parameter Specifications
-
\c{(10 points) Suppose that you are trying to help a marketing manager come up with the largest possible number to use to advertise the field of view offered by their new head-mounted display device. if the vertical field of view is
90^\circand the horizontal field of view is110^\circwhat is the diagonal field of view?}The relationship between FOV angle and the length (whichever way we're measuring) is
\tan(\frac{1}{2} \theta) = \frac{L}{2d}, wheredis the distance the viewer is from the screen.Because the viewer will remain the same distance from the screen while all these calculations are being made, we can just ignore it completely by setting it to 1. So we have
\tan(\frac{1}{2} \theta) = \frac{L}{2}.Now, we can find
wandhby reversing this into $L = 2\tan(\frac{1}{2} \theta)$:w = 2\tan(55^\circ)h = 2\tan(45^\circ)
The diagonal
Dcan be calculated using Pythagorean's theorem:-
$D = \sqrt{w^2 + h^2} = 2\sqrt{\tan^2(55^\circ) + \tan^2(45^\circ)} \approx 3.48$
In [68]: w = 2 * tan(radians(55)) In [69]: h = 2 * tan(radians(45)) In [71]: sqrt(pow(w, 2) + pow(h, 2)) Out[71]: 3.486893591242196
Now, we can convert this length back into an angle by turning the original equation around:
\theta = 2\tan^{-1}(\frac{1}{2} L), which gives us a value of around120^\circ.In [72]: 2 * atan(0.5 * _) Out[72]: 2.1000651019312633 In [73]: degrees(_) Out[73]: 120.32486704337242
Geometry for Computer Graphics
-
\c{(4 points) Consider a triangle defined by the vertices: $v_0 = (0, 1, 2), v_1 = (4, 1, -2), v_2 = (2, 2, 0)$, specified in counter-clockwise order. What is the area of this triangle?}
The area of a triangle given two of its sides is $\frac{1}{2} |e_1 \times e_2|$. In this case,
e_1 = v_1 - v_0 = (4, 0, -4), and $e_2 = v_2 - v_0 = (2, 1, -2)$.The cross product is (4, 0, 4) (I used numpy to calculate this, see below output), which normalizes to
\sqrt{32}. Half of this is\boxed{\sqrt{8}}, which is the area.In [2]: v0 = np.array([0,1,2]) In [3]: v1 = np.array([4,1,-2]) In [4]: v2 = np.array([2,2,0]) In [5]: e1 = v1 - v0 # (4, 0, -4) In [6]: e2 = v2 - v0 # (2, 1, -2) In [8]: np.cross(e1, e2) Out[8]: array([4, 0, 4])
Point-in-Polygon Testing
-
\c{Consider a triangle defined by
v_0 = (3, 0, -2),v_1 = (2, 4, 0), $v_2 = (-2, 2, 2)$, in counterclockwise order, and a pointp = (2, 1, -1).}a) \c{(9 points) What are the barycentric coordinates that define the location of the point
pwith respect to the locations ofv_0,v_1, andv_2?}Using
v_0as the base, we can writee_1 = v_1 - v_0 = (-1, 4, 2), ande_2 = v_2 - v_0 = (-5, 2, 4). We also neede_p = p - v_0 = (-1, 1, 1). Now we can proceed to find\betaand\gamma.Using the above, we get:
d_{11} = e_1 \cdot e_1 = (-1, 4, 2) \cdot (-1, 4, 2) = 1 + 16 + 4 = 21d_{12} = e_1 \cdot e_2 = (-1, 4, 2) \cdot (-5, 2, 4) = 5 + 8 + 8 = 21- $d_{22} = e_2 \cdot e_2 = (-5, 2, 4) \cdot (-5, 2, 4) = 25 + 4 + 16 = 45$
d_{1p} = e_1 \cdot e_p = (-1, 4, 2) \cdot (-1, 1, 1) = 1 + 4 + 2 = 7d_{2p} = e_2 \cdot e_p = (-5, 2, 4) \cdot (-1, 1, 1) = 5 + 2 + 4 = 11
Plugging this into the formula, we get:
\begin{align*} \begin{bmatrix} e_1 \cdot e_1 & e_1 \cdot e_2 \ e_1 \cdot e_2 & e_2 \cdot e_2 \ \end{bmatrix} \begin{bmatrix} \beta \ \gamma \end{bmatrix} &= \begin{bmatrix} e_1 \cdot e_p \ e_2 \cdot e_p \end{bmatrix} \ \begin{bmatrix} 21 & 21 \ 21 & 45 \end{bmatrix} \begin{bmatrix} \beta \ \gamma \end{bmatrix} &= \begin{bmatrix} 7 \ 11 \end{bmatrix} \ \end{align*}
Checking the determinant $\det \begin{vmatrix} 21 & 21 \ 21 & 45 \end{vmatrix} = 21 \times 45 - 21 \times 21 = 504$, which is non-zero. This means the matrix is invertible and we can solve for
\betaand\gamma. Now we have:- $\beta = (d_{22} d_{1p} - d_{12} d_{2p}) / \det = (45 \times 7 - 21 \times 11) / 504 = \frac{1}{6}$
- $\gamma = (d_{11} d_{2p} - d_{12} d_{1p}) / \det = (21 \times 11 - 21 \times 7) / 504 = \frac{1}{6}$
Then,
\alpha = 1 - (\beta + \gamma) = \frac{2}{3}.b) \c{(1 point) Does p lie: inside the triangle; outside of the triangle; or on the edge of the triangle? (please circle the correct answer)}
Using these values, we can see that all three values lie between 0 and 1, which means the point is definitely inside the triangle.
Smooth Shading
-
\c{(6 points) Consider a triangle defined by
v_0 = (1, 1, -2), $v_1 = (-1, 0, 1)$,v_2 = (2, -1, -1), in counter-clockwise order, where the associated normal directions are:vn_0 = (\frac{2}{3}, -\frac{2}{3}, \frac{1}{3}),vn_1 = (-\frac{2}{3}, \frac{1}{3}, \frac{2}{3}), $vn_2 = (-\frac{1}{3}, \frac{2}{3}, \frac{2}{3})$. If the barycentric coordinates\alpha = 0.3,\beta = 0.6,\gamma = 0.1describe the location ofpwith respect tov_0,v_1,v_2, what is the smooth-shading surface normal direction atp(interpolated from the vertex normals) that should be used when computing the Phong illumination atp?}This is simply applying each of the barycentric coordinates (which is really just a weight of how close
pis to a particular vertex) to the corresponding vertex, and summing them. The corresponding vertex is the one opposite from the side that the coordinate defines.\begin{align*} n &= \alpha \cdot vn_0 + \beta \cdot vn_1 + \gamma \cdot vn_2 \ &= 0.3 \cdot vn_0 + 0.6 \cdot vn_1 + 0.1 \cdot vn_2 \ &= 0.3 \cdot \left(\frac{2}{3}, -\frac{2}{3}, \frac{1}{3} \right) + 0.6 \cdot \left(-\frac{2}{3}, \frac{1}{3}, \frac{2}{3} \right) + 0.1 \cdot \left(-\frac{1}{3}, \frac{2}{3}, \frac{2}{3} \right) \ &= (0.2, -0.2, 0.1) + (-0.4, 0.2, 0.4) + \left(-\frac{0.1}{3}, \frac{0.2}{3}, \frac{0.2}{3} \right) \ &= \boxed{(-0.2\overline{333}, 0.0\overline{666}, 0.5\overline{666})} \end{align*}
Phong Illumination
-
\c{(10 points) Suppose you are rendering a simple scene that contains a single sphere of radius 3 centered at (0, 0, 0) and illuminated by a single white point light source located at (0, 4, 2). Use the Blinn-Phong illumination model to determine what color a viewer at (6, –2, 3) will perceive at the point
p = (2, 2, 1)if the material properties of the sphere arek_a = 0.2,k_d = 0.6,k_s = 0.3,n=2, $O_{d\lambda} = (1, 0, 0)$ andO_{s\lambda} = (1, 1, 0). Please provide the(r, g, b)color definition and also name the color that this value corresponds to.}First, we have to find some vectors needed for the Blinn-Phong equation:
- For the normal
\vec{N}, we can just subtract the sphere center from the intersection point, yielding\vec{N} = (2, 2, 1). - For the vector to the viewer
\vec{V}, we can subtract the intersection point from the viewer location, yielding $\vec{V} = (6, -2, 3) - (2, 2,- = (4, -4, 2)$.
- For the light direction
\vec{L}, subtract the intersection point from the light\vec{L} = (0, 4, 2) - (2, 2, 1) = (-2, 2, 1). - The halfway direction is just halfway between the light and the viewer, which is $\vec{H} = (\vec{L} + \vec{V}) / 2 = ((-2, 2, 1) + (4, -4, 2)) / 2 = (2, -2, 3) / 2 = (1, -1, 1.5)$.
First, substitute the values given into the Blinn-Phong equation:
\begin{align*} I_\lambda &= k_a O_{d\lambda} + k_d O_{d\lambda} (\vec{N} \cdot \vec{L}) + k_s O_{s\lambda} (\vec{N} \cdot \vec{H})^n \ I_\lambda &= 0.2 \cdot (1, 0, 0) + 0.6 \cdot (1, 0, 0) ((2, 2, 1) \cdot (-2, 2, 1)) + 0.3 \cdot (1, 1, 0) ((2, 2, 1) \cdot (1, -1, 1.5))^2 \ I_\lambda &= (0.2, 0, 0) + (0.6, 0, 0) \cdot (-4 + 4 + 1) + (0.3, 0.3, 0) (2 - 2 + 1.5)^2 \ I_\lambda &= (0.2, 0, 0) + (0.6, 0, 0) + (0.3, 0.3, 0) \cdot 2.25 \ I_\lambda &= (0.8, 0, 0) + (0.675, 0.675, 0) \ I_\lambda &= (1.475, 0.675, 0) \ \end{align*}
We clamp to 1, so the result is
\boxed{(1, 0.675, 0)}. This is an orange-ish brown color. - For the normal
Ray-Object Intersection
-
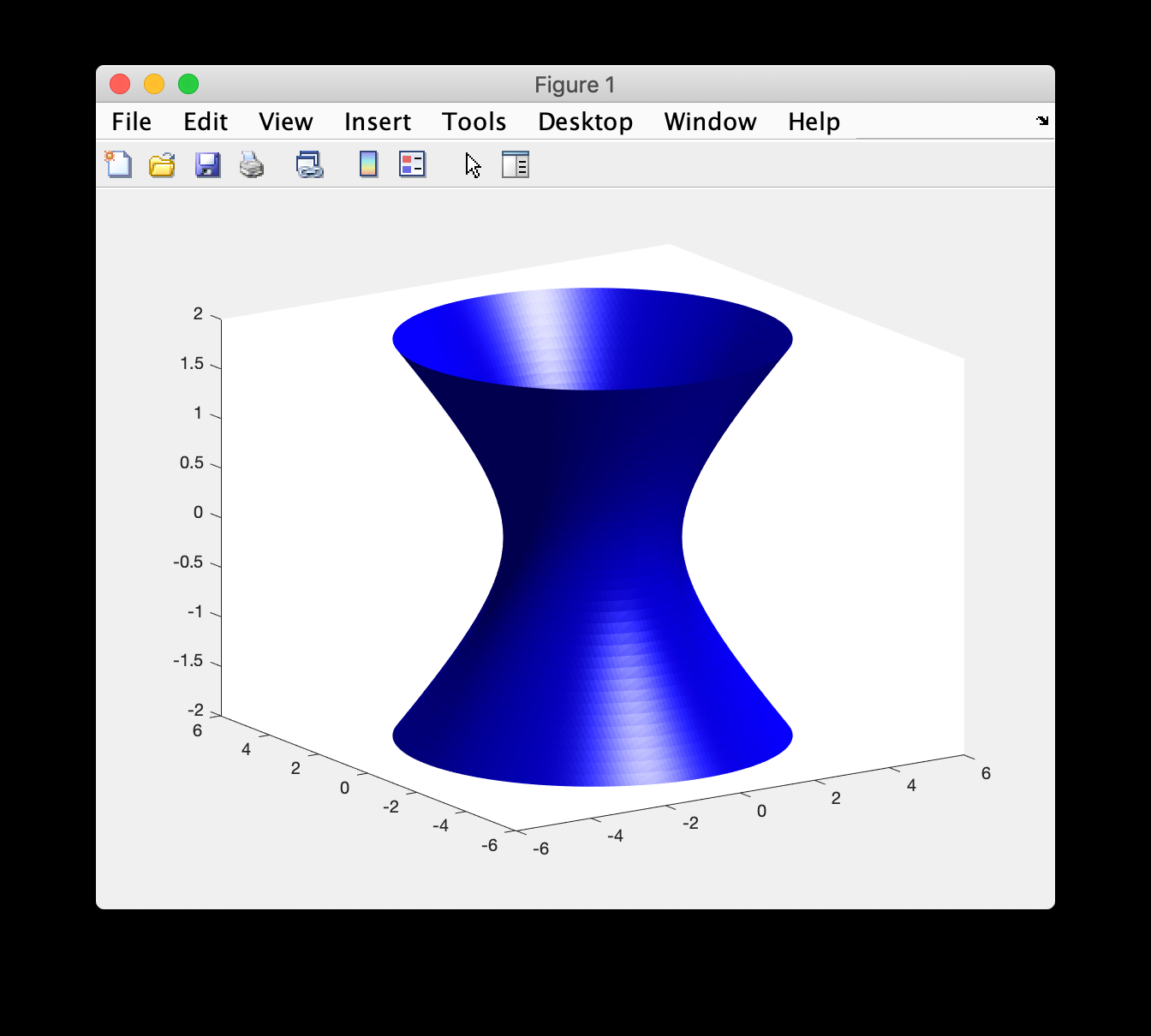
\c{(14 points) The set of all points on the surface of an infinite, circularly symmetric, one-sheet hyperboloid, centered at the origin and aligned with the z axis, can be defined by the implicit equation:
\frac{x^2}{r^2} + \frac{y^2}{r^2} - \frac{z^2}{c^2} = 1whererandcare parameters that control the radius and curvature of the hyperboloid, and the set of all points(x, y, z)for which the implicit equation is true lie on the surface of the hyperboloid. Letr = 2andc = 1, to obtain the surface shown at the right.}\c{Consider a viewing ray that starts at
p_0 = (-2, 1, -1)and travels in the directiond = (0, 1, 1). Does this ray intersect this surface? If so, at what point(s)?}Starting by substituting in the ray equation, we would get:
\begin{align*} \frac{(x_0 + tx_d)^2}{r^2} + \frac{(y_0 + ty_d)^2}{r^2} - \frac{(z_0 + tz_d)^2}{c^2} &= 1 \ \frac{x_0^2 + 2tx_0x_d + t^2x_d^2}{r^2} + \frac{y_0^2 + 2ty_0y_d + t^2y_d^2}{r^2} - \frac{z_0^2 + 2tz_0z_d + t^2z_d^2}{c^2} &= 1 \ \left( \frac{x_d^2}{r^2} + \frac{y_d^2}{r^2} - \frac{z_d^2}{c^2} \right) t^2 + 2 \left( \frac{x_0x_d}{r^2} + \frac{y_0y_d}{r^2} - \frac{z_0z_d}{c^2} \right) t + \left( \frac{x_0^2}{r^2} + \frac{y_0^2}{r^2} - \frac{z_0^2}{c^2} - 1 \right) &= 0 \end{align*}
Then, substituting in the values for
r,c, and the ray parameters gives:\begin{align*} \left( \frac{0^2}{2^2} + \frac{1^2}{2^2} - \frac{1^2}{1^2} \right) t^2 + 2 \left( \frac{-2 \cdot 0}{2^2} + \frac{1 \cdot 1}{2^2} - \frac{-1 \cdot 1}{1^2} \right) t + \left( \frac{(-2)^2}{2^2} + \frac{1^2}{2^2} - \frac{(-1)^2}{1^2} - 1 \right) = 0 \ \left( 0 + \frac{1}{4} - 1 \right) t^2 + 2 \left( \frac{1}{4} + 1 \right) t + \left( 1 + \frac{1}{4} - 1 - 1 \right) = 0 \ -\frac{3}{4} t^2 + \frac{5}{2} t -\frac{3}{4} = 0 \end{align*}
Now we can just use quadratic equation with
A = -\frac{3}{4}, $B = \frac{5}{2}$, andC = -\frac{3}{4}. Quickly checking the determinant $B^2 - 4AC = \frac{5}{2}^2 - 4 \cdot (-\frac{3}{4})^2 = \frac{25}{4} - \frac{9}{4} = \frac{16}{4} = 4$, which is positive so there are \boxed{\textrm{two solutions}}.To get the points themselves, we solve for
t:\begin{align*} t &= \frac{-\frac{5}{2} \pm \sqrt{4}}{2 \cdot -\frac{3}{4}} \ t &= \frac{-\frac{5}{2} \pm 2}{-\frac{3}{2}} \ t &= \frac{-5 \pm 4}{-3} \ t &\in {\frac{1}{3}, 3} \end{align*}
Now, just substitute the
tback into the ray equationp = p_0 + dtto get\begin{align*} p_0 &= (-2, 1, -1) + \frac{1}{3} (0, 1, 1) \ &= (-2, 1, -1) + (0, \frac{1}{3}, \frac{1}{3}) \ &= (-2, \frac{4}{3}, -\frac{2}{3}) \end{align*}
\begin{align*} p_1 &= (-2, 1, -1) + 3 (0, 1, 1) \ &= (-2, 1, -1) + (0, 3, 3) \ &= (-2, 4, 2) \end{align*}
The ray intersects the hyperboloid at \boxed{(-2, \frac{4}{3}, -\frac{2}{3}) \textrm{and} (-2, 4, 2)}.
Texture Mapping
-
\c{(10 points) Suppose that a texture image has been mapped onto the surface of a truncated cylinder such that the values of
uincrease from 0 to 1 as the values of\thetaincrease from0to2\pi, and the values ofvdecrease from 1 to 0 as the position along the cylinder’s height increases from its base to its top. Consider a cylinder of radius 2 and height 4, whose base is centered at(0, 0, 0). What is the texture coordinate $(u, v)$ at the pointp = (-\sqrt{2}, \sqrt{2}, 1)?}The point
(-\sqrt{2}, \sqrt{2})occurs at\theta = \frac{3}{4}\pi, so when mapped tou, this corresponds to a value ofu = \frac{3}{8}.The height of 1 occurs halfway on the cylinder, which corresponds to a $v = 0.5$.
The coordinate is
\boxed{(\frac{3}{8}, 0.5)}. -
\c{Consider a texture image that is 1024 pixels wide and 512 pixels tall. If bi-linear interpolation is used to retrieve a color from this image corresponding to the texture coordinate (u, v) = (0.6, 0.2):}
a) \c{(4 points) From which four pixels
[i, j]in the image will the texture colors be retrieved?}Multiplying it out, we get the exact coordinates (0.6 * 1024, 0.2 * 512) = (614.4, 102.4). This means, we will be sampling from:
- (614, 102)
- (614, 103)
- (615, 102)
- (615, 103)
b) \c{(6 points) Suppose that the colors in the texture image have been defined to be white when
iandjare both even numbers, red wheniis even andjis odd, green wheniis odd andjis even, and blue when bothiandjare odd. What color will be returned from the texture lookup, after the retrieved colors have been appropriately combined using bilinear interpolation?}Using this information, the colors corresponding to each of the above are:
- (614, 102): white
- (614, 103): red
- (615, 102): green
- (615, 103): blue
Then, we need to weigh these according to how close the point we want to observe is from those four corners:
- (614, 102): 0.6 * 0.6 * (1, 1, 1) = 0.36 * (1, 1, 1) = (0.36, 0.36, 0.36)
- (614, 103): 0.6 * 0.4 * (1, 0, 0) = 0.24 * (1, 0, 0) = (0.24, 0, 0)
- (615, 102): 0.4 * 0.6 * (0, 1, 0) = 0.24 * (0, 1, 0) = (0, 0.24, 0)
- (615, 103): 0.4 * 0.4 * (0, 0, 1) = 0.16 * (0, 0, 1) = (0, 0, 0.16)
Taking the sum, we get (0.36 + 0.24, 0.36 + 0.24, 0.36 + 0.16) = \boxed{(0.6, 0.6, 0.52)}.